超詳解 3 大類 9 款去中心化金融固定利率協議運作模式與使用情境

Author：
Ethan Chen, Researcher of EM3DAO, EVG, Hakka Finance
Lucien Lee, CEO of Hakka Finance
Ping Chen, Founder of Hakka Finance

---

DeFi 的發展日新月異，交易和借貸是最重要的兩大支柱。

在交易方面，金融史上前所未有的 AMM 模式勝過了 orderbook，成為鏈上流動性的典範；而借貸這邊也從 p2p lending 全面轉向 p2pool 的模式。Aave 的前身 Ethlend 向我們示範了 orderbook 方式的 p2p 借貸模式，雖然有著明確到期日及固定利率的好處，但在沒有足夠流動性，配對效率極為低下，因此被 DeFi 市場給淘汰。取而代之的是 Compound、Aave 等由供需控制利率的永續資金池借貸模式。

然而，少了到期日，借貸需要靠別的力量來維持供需均衡，在 lending pool 中便是「利用率 - 利率」的回授控制機制：供不應求的時候升息，鼓勵存/還款；供過於求的時候降息，鼓勵借/提款。儘管 Aave 號稱有固定利率借款功能，但其實還是對固定利率借款保有調高利息的機制。可以說利率浮動是永續借貸資金池的必然現象。

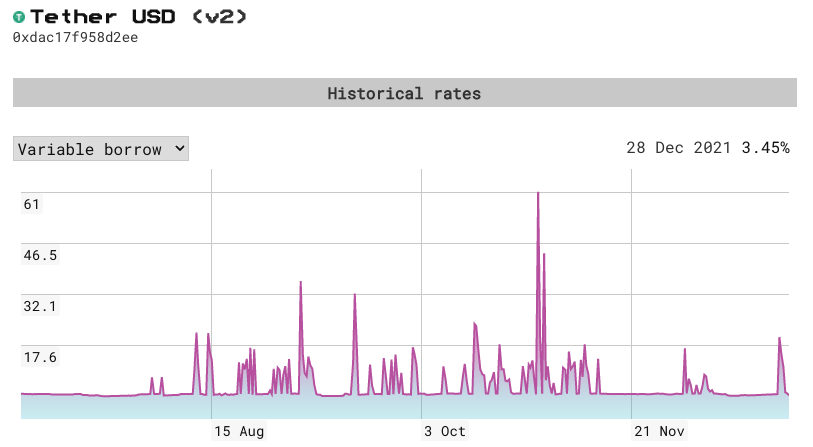
同時借貸做為建構投資組合的基礎元件，通常被期待擁有可預測的利率，譬如以固定收益產品，如不動產抵押債券、公共債券為基底，組成的保本型基金，或者以固定利率借款的比特幣槓桿倉位。可預測利率可以說是發展現代化金融商品的基石。

撰寫本文時， DeFi 借貸協議的未償債務總額約為 236 億美元。相比之下，全球債務市場估計為 128萬億美元，隨著更多使用者與機構進入 DeFi 市場，固定利率的需求絕對是持續蓬勃增長。因此，我們大膽預測，固定利率協議將成為 DeFi 的新聖杯，也會是下一波 DeFi 爆發成長不可或缺的基石。

DeFi 中的固定利率機制

DeFi 是利率收益資產（Yield）繁星交織輝煌的銀河，不論是借貸、AMM LP 交易手續費、流動性挖礦、收益聚合⋯⋯等等，DeFi 四處充斥利率收益資產，而區塊鏈上的利率都是由市場力量動態決定，因此他無時無刻都在浮動。為了因應市場對於不同風險的偏好，因此有許多產品嘗試打造固定利率 DeFi 產品，而其中又以固定利率借貸為最大宗，使用者希望存款時能提早掌控未來的收益，或於借款時就確定借款成本，以免因市場波動而使借款成本超出預期。本文將涵蓋 Yield Protocol, Notional Finance, HiFi, Pandle Finance, Element Finance, Swivel, Sense Protocol, Barnbridge, Tranche 等 9 種固定利率協議，各個協議形成固定利率的方式都不同，接著我們將根據使用的機制對它們進行分類。

機制總覽

首先，最關鍵的就是「固定利率」的來源。前述提到 Compound/Aave deposit 等浮動利率是源自 lending pool 的供需力量起落，若一個人要得到不受市場波動影響的固定收益時，勢必得擺脫跟池子交易的模式，找到另一人做為對手，提出支付一定利息的保證。而這樣的保證利息來源有兩種：一種是由借方支付固定利息，另一種是透過貸方的利息重分配來達成。

1. 固定利率借貸： Fixed-rate Loan

由借方支付固定利息的方式本質上和 Bitfinex 放貸相去不遠，都是透過約定日期、約定額度、固定利率的方式進行借貸，只是改用一些比較適合區塊鏈的方式，譬如將 p2p 借貸改為 p2pool，透過 AMM 借貸做價格（利率）發現。

一種實現此目的之機制為「交易零息債券」。零息債券（Zero coupon bond）是不支付利息的債券，但通常他的交易價格會低於面值，到期後會按面值支付給債券持有人。貸方以折價購買零息債券相當於固定利率存款，可於到期日時領取面額上的資金，而借方則可透過抵押資產來借出零息債券並折價賣成現金，想取回抵押品需於到期日後歸還零息債券上面額的欠款，從系統借出之零息債券面額和賣出後得到之現金的差即為借款利息。由於借款的成本即為存款的收益，因此可透過市場供需達到均衡，來決定借貸雙方都能接受的固定利率。

舉例來說，借方抵押資產後發行一張一年期的面額 $1,100 零息債券，然後在市場上以 $1,000 折價賣給貸方。貸方相當得到一年期固定利息 10% 的 $1,000 債權，而到期時借方必須支付票面面額 $1,100 去贖回零息債券，對借方來說，他也得到了一年期固定利息 10% 的 $1,000 借款。 用零息債券設計固定利率的好處在於，因為零息債券因為沒有利息，所以不像有息債券會面臨再投資風險。也就是當你領到利息後，將賺到的利息再重新投資時，因為市場利率隨時都在變動，你的總收益也因此不可預期，得承擔市場利率變動的風險。可以說零息債券是一個在購買當下，就能完全確定收益的投資工具。

相關協議：Yield Protocol, Notional Finance, HiFi

2. 利息重分配： Yield Redistribution

前者本質上是一個獨立的借貸市場，而另一種方式則是基於既有的利息來源，可以是浮動利率的存款，也可以是 Yield Farming，衍生出一個交易利率的次級市場。而根據交易模式不同，又可以再分成本金-利息拆分與結構型商品兩種。

2–1. 本金-利息分離 (Split Principal & Interest)

給定一個收益來源，我們可以將投資的回報拆分成本金和利息兩部分，並分別定價。比方說，你可以將「存進 Aave 的 $10,000 USDC 一年後會賺到的利息」做為一個商品販售，如果有人願意出 $400 USDC 買它，那你實際上就得到了一個 4% 的固定收益投資。你也可以理解成 A 和 B 兩人分別出 $9,600 和 $400 一起投資到 Aave，並約好一年後 A 拿 $10,000 而 B 拿到剩下的部分，達到事先約定利潤分配的效果。實現以上目的之作法為，將借貸協議中的本金和利息拆分，並將兩者皆代幣化。利息代幣在結算前的定價取決於市場對未來利率的預期，而本金代幣則相當於零息債券，能於到期日後按面額贖回資產，在到期日前零息債券會根據該資產在市場中的時間價值而產生折價。

從以上的例子，很容易理解本息分離如何做到固定利率貸款，另一方面若要做到固定利率借款，可以透過在借款當下買入利息代幣，理論上只要借款與貸款利率之間的波動相關性非常緊密，借款的利息浮動會被貸款的利息代幣的價值浮動相消，因此達成固定利率借款的效果。而實際上借/貸款利率走勢之間，根據資金使用率的狀況，並不一定完全相同，因此只會達成部分對沖效果。

相關協議：Element Finance, Pendle Finance, Swivel, Sense Protocol

2–2. 結構型商品 (Structured Product)

在借貸協議中存款利息的大小為浮動的，既然未來利息具不確定性，且每個人有著不同的風險承受能力和資金的機會成本，那就可以將根據個人的需求去重新分攤風險。

結構型基金可針對投資人對市場預期的不同，將利息收益拆分成不同等級，並將其重新組合成不同的金融衍伸品。

它本質上是一種融資槓桿，但因為販售固定利率債券的收入通常也會被用於增持相同的變動利率資產，所以實際上的效果和本金-利息拆分類似，也是一種利率的再分配。

舉例來說，我們可以設計一個以 5% 為界的雙層架構基金，Ａ類為風險較低但優先收益分配的產品（固定利率），B 類為風險較高但高收益的產品（浮動利率），基金的錢全部都拿去 Aave 裡放貸，若最終累積利息超過 5%，A類投資人只能拿約定好的 5% 收益，而 B 類投資人可以拿其餘的超額報酬。反之不到 5% 時， B 類投資人的錢會拿去填補 A 類投資人利息不足 5% 的部分，直到 B 類投資人的投資全部賠空。

相關協議：BarnBridge, Tranche

---

各協議介紹

固定利率借貸

在 DeFi 中實現固定利率借貸最容易的方式是透過鑄造/購買零息債券。

零息債券是一種借據，發行商承諾持有人可以在到期日時以 1:1 換回面額價值的資金，但由於資金具時間價值，因此在到期日之前零息債券會折價在市場上流通，折價的大小則由市場利率以及到期時間而異，折價越大代表到期時之收益越高，反之亦然。

貸方以折價購買零息債券，並於到期日時按面額大小贖回資產，相當於以固定利率借款；而零息債券則是由借款方所提供，借方先以超額抵押資產後，再鑄造出零息債券並賣成現金，以達成固定利率借款的效果。

各家差異主要在於零息債券如何用適合區塊鏈的方式定價，我們將在後面 AMM 章節深入討論。

Yield Protocol

Yield Protocol 為使用零息債券 (fyDai) 作為實現固定利率借貸的協議，在到期日之後 fyDai 能以 1:1 贖回 Dai。

固定利率存款和借款的機制如下：

• 固定利率存款：先以折價購買零息債券 (fyDai) 在於到期日後贖回，收取固定利息。

例如：Alice 以 1000 Dai 購入 1050 fyDai，若一年後到期，屆時可換回 1050 Dai，相當於 5% 固定年化存款利率。

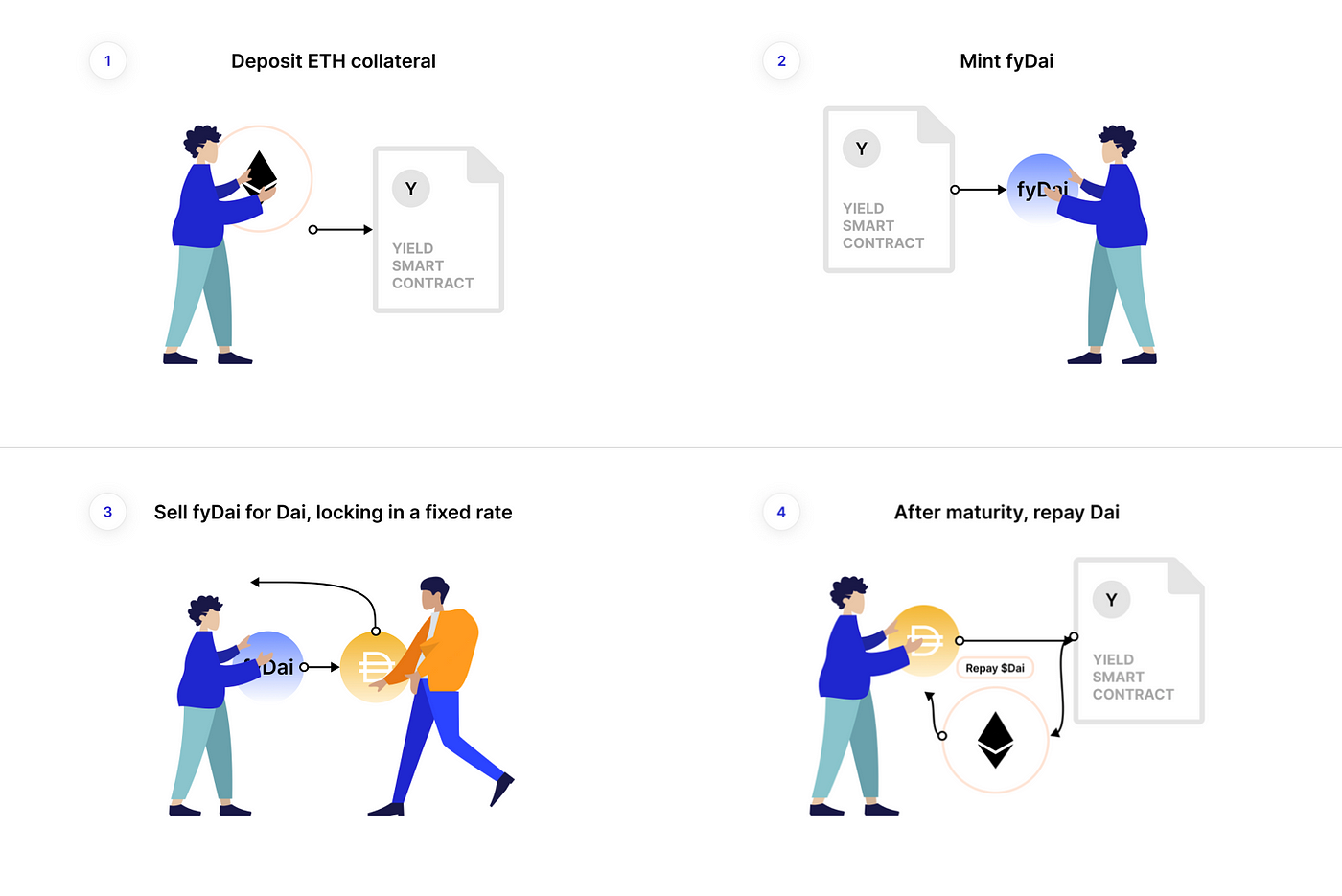
• 固定利率借款：先存入 ETH 當抵押品，並鑄造出 fyDai 再賣成 Dai，由於 fyDai 會折價，因此拿到的 Dai 數量變少，兩者之差額即為預先鎖定的借款成本。

例如：Bob 在協議中抵押 1 ETH，以 5% 年化借出 1000 個 Dai，若到期日為一年後，代表 Bob 欠系統 1050 fyDai，需歸還欠款後才能贖回抵押物。

值得一提的是，在 Yield Protocol V1 中整個服務搭建於 MakerDAO 上，因此能於到期日之後，將整個借貸的倉位轉移至 MakerDAO 內，使固定利率轉為浮動利率，此時存款方能收取 Dai Saving Rate，而借款方則需支付 stability fee。

而在新版的 V2 中則捨棄了與 MakerDAO 的連動，但也因此打破了 MakerDAO 的限制，得以支援更多的抵押品，包含 yvUSDC、ENS 等，並能支援其他幣種的借款，如 USDC。

此外，由於零息債券的價值會隨時間變動，因此 Yield Protocol 創造出了一條新的 AMM 曲線 YieldSpace，該曲線之特殊性質適合作為零息債券的流動池，還能提高資金效率，已成為相關協議之 AMM 標準。

流動性倉位管理
由於每一期的零息債券都有不同的到期日和價格，因此每期皆需有獨立的流動池以供人交易。 目前 Yield Protocol 每一期為六個月，為了不讓流動性提供者頻繁的調倉，流動性會於到期後被自動轉至最新的一期，如此一來流動性提供者無需花費 gas fee 即可持續賺取手續費。

Notional

Notional 同樣以交易及抵押鑄造零息債券 (fCash) 來達成固定利率借款，借貸利率由市場供需來決定。

與 Yield Protocol 最大不同的地方在於，Notional 系統中的底層資產為 cToken，也就是 Compound 的存款憑證，交易零息代幣的流動池為 fCash/cToken，使流動池中存放的資金都能隨時間產生利息，增加流動性提供者之資金使用效率。

固定利率存款和借款的機制如下：

• 固定利率存款：存款方支付 DAI，系統會先將其存入 Compound 中換得 cDAI，再至流動池中購買零息債券 fDAI，購買的價格即決定了固定借款利率之大小。
• 固定利率借款：抵押 ETH 之後，可鑄造出 fDAI，再將其賣成 cDAI，最終至 Compound 取回 DAI 以實現固定利率借款，fDAI 和 DAI 之差為借款成本。

由於池內底層資產為 cToken，因此在到期日後存款之固定利率會自動轉變成 Compound 的浮動利率。

流動性統一管理
在 Notional 中的底層資產為 cToken，雖然協議中同時會有很多期的零息債券，但想做為流動提供者僅需於於統一的入口存入 cToken，系統會將集中的流動性自動分配至各個池內，實際分配的比例則由社群治理來決定。

如此一來，流動性提供者無需隨到期日頻繁換池，協議也可透過治理的方式最大化資金使用效率。

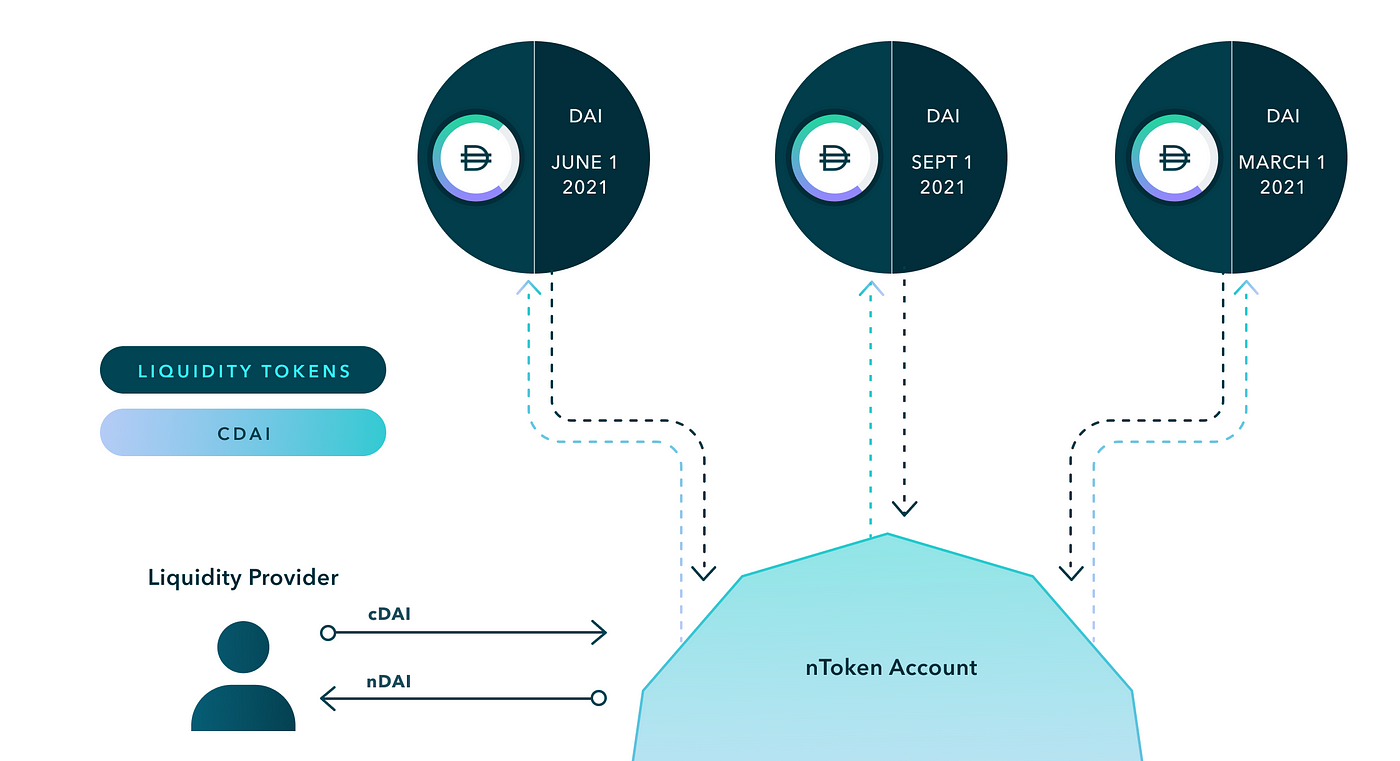
存入 cToken 後會拿到 nToken 作為憑證，該憑證無到期日，隨時可贖回。而存入的 cToken 會有一部分被用於購買 fCash，並以 fCase 和 cToken 組合成流動性，因此 nToken 的混合利率 (blended interest rate) 會介於零息債券和 Compound 的存款利率之間。

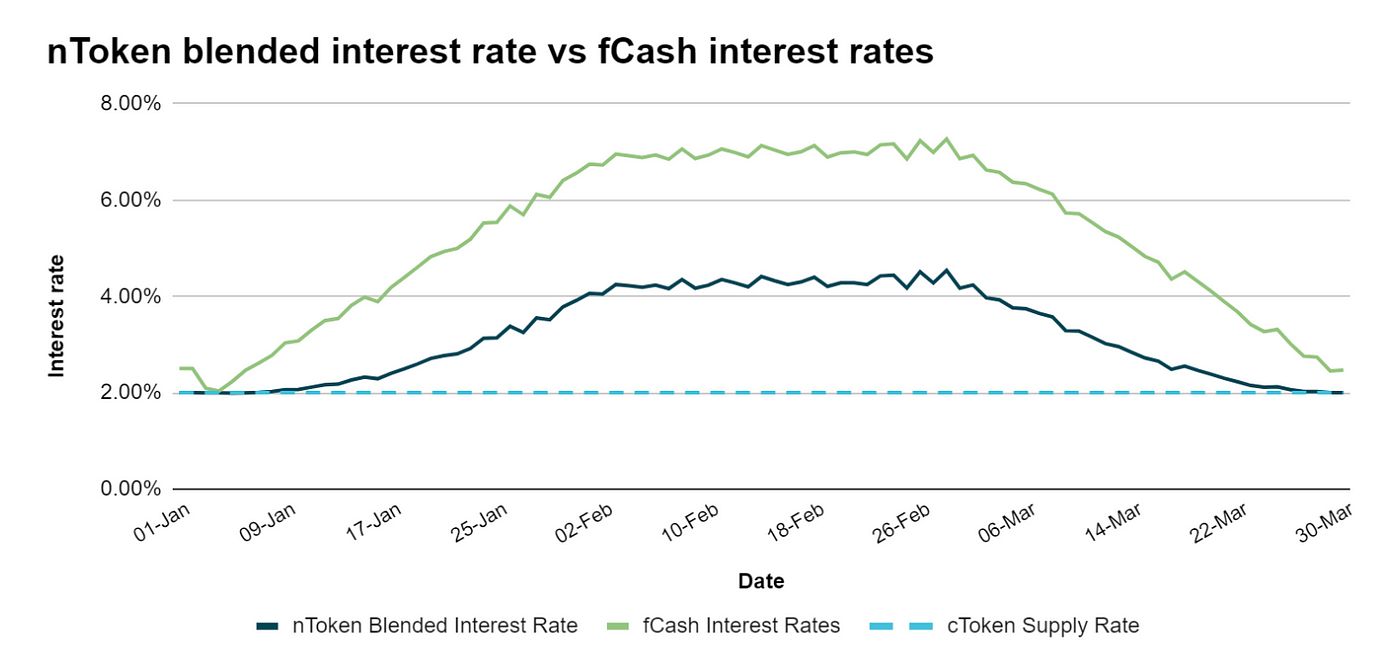
雖然作為流動性提供者的利率會低於直接購買零息債券 (fCash)，但優點是還可賺取交易手續費。此外，Notional 還支援以 nToken 作爲抵押品，使流動性提供者可存入 nToken 並借出資產，再重複將該資產投入流動性以換得更多的 nToken，以槓桿（類似 Alpha）加大流動性提供者的收益。

HiFi

HiFi Finance 前身為 Mainframe ，是一樣利用零息債券的固定利率借貸協議，原理上與 Yield 並無二致。都是透過借方抵押資產，借出零息債券，賣給貸方來達成固定利率的效果。在他們 v0 版的白皮書中，比較特別的地方在於，留有清算擔保池能直接為清算抵押率不足的債務（類似於 liquity 的機制），另外清算擔保池與借款抵押品，也能用於閃電貸（flash loan）賺取收益，讓閒置資金獲得更多利用。

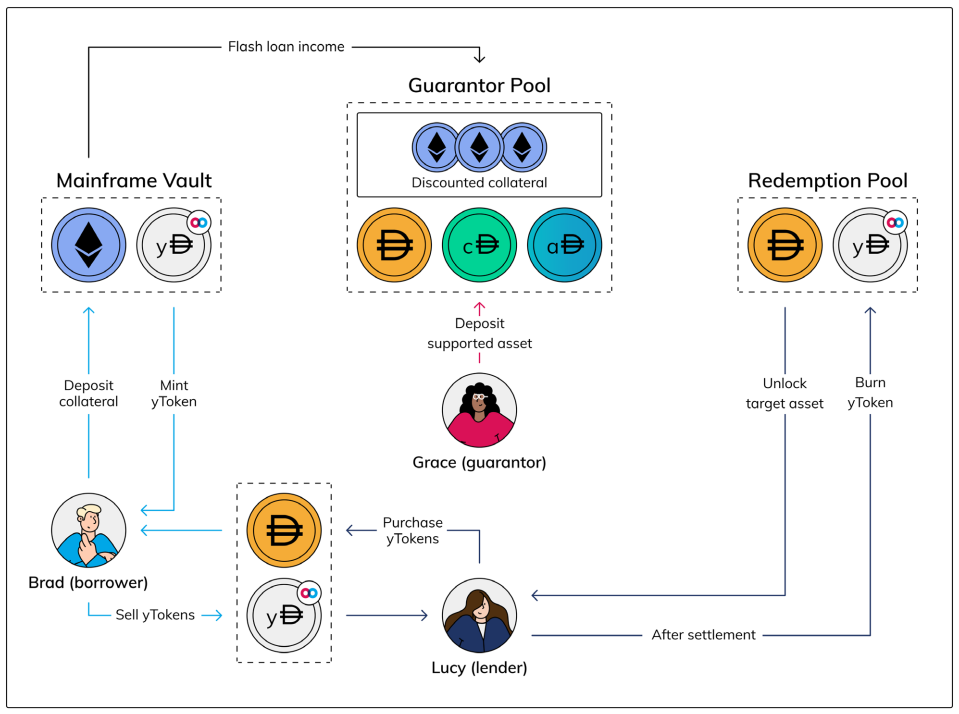
然而，目前 HiFi v1 的設計上，已經跟 Yield 毫無差異。不僅 AMM 模型基於 YieldSpace，同時清算擔保池的設計也不見蹤影。取而代之的是，提供腳本工具讓清算者使用 Uniswap v2 閃電換（Flash swaps）清算債務，而這也與其他產品十分類似。

---

利息重分配

如前章所述，將借款憑證作為零息債券，再以折價賣給存款方即可實現固定利率借貸，此時利息的來源為借貸雙方於市場中搓合之結果。

而另種實現固定利率的做法為，將系統內所有資金都先存入借貸協議或是收益聚合器領取浮動利率，再根據每個人的風險偏好去重新分配利息。

此種重新分配貸方利息的做法，又可分成「本金-利息代幣分離」以及「結構型商品」二類，各相關協議之介紹如下：

本金 - 利息分離

將資金存入借貸協議或收益聚合器中之後，我們可把存入的本金和未來的利息拆分，並將其代幣化。

本金代幣可於到期日後按 1:1 贖回底層資產，雖然在此模式中無借款行為，但其性質仍可等效於零息債券；而利息代幣代表的則是未來會產出的利息，兌現未來利息之機制因協議而異。

各家差異主要在於本金代幣和利息代幣如何用適合區塊鏈的方式定價，我們將在後面 AMM 章節深入討論。

其中利息代幣又分為以下兩種模式

• Drag — 已實現利息會累積到期時才能領取 (Past yield delivered at maturity)
• Collect — 已實現利息不斷轉移給持有者 (Past yield delivered before maturity)

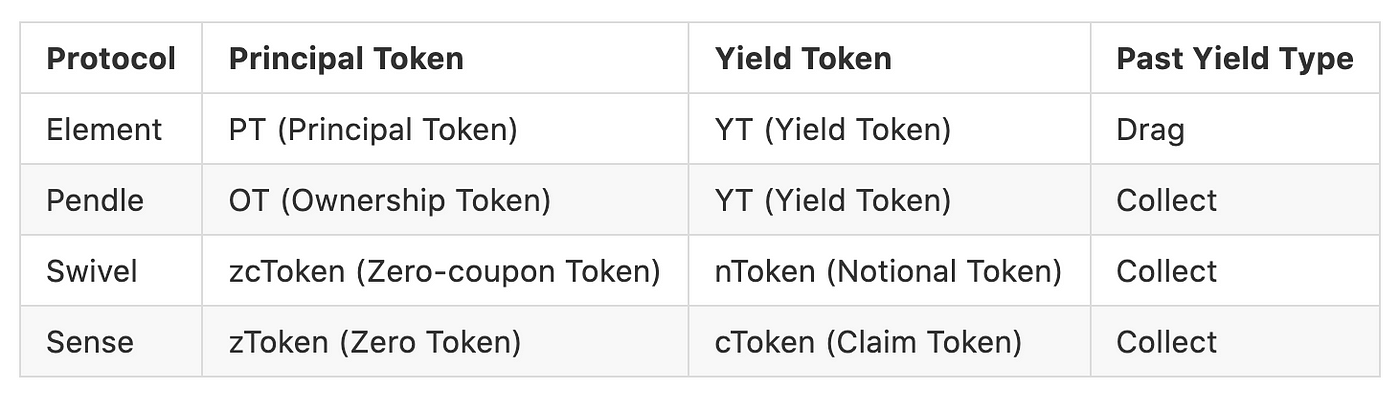
Element

在 Element 中所有的資金會存入 Yearn Finance 內，並將存入的資金拆分成本金代幣 (PT, Principal Token) 和利息代幣 (YT, Yield Token)。

本金代幣相當於零息債券，可於到期日後將本金部位贖回；而利息代幣則代表未來利息，可於到期日後兌換出期間實際產生之利息。

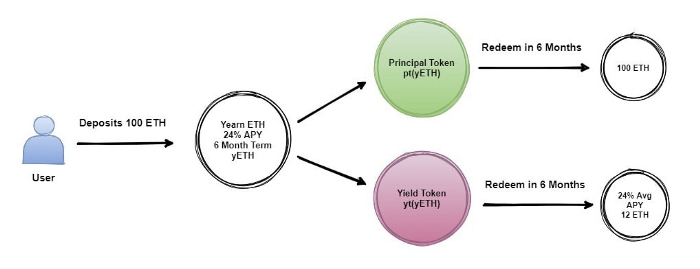
在此系統下，我們可以創造出「固定利率存款」和「槓桿做多利率」的市場

• 固定利率存款
  購買本金代幣相當於以固定利率存款，而年化的大小由本金代幣的價格來決定，價格越小代表到期時的獲利越多，年化利率越高，反之亦然。

另一種作法為在 Element 中存入資金後，直接將鑄造出來的 YT 賣掉，提早變現未來利息以實現固定利率收益。

• 槓桿作多未來利率
  利息代幣 (YT) 的價格代表市場對未來利息的預期，而期間累積利息越高 YT 的結算價就越高。

我們能透過購買 YT 來槓桿做多利率，只要於到期日後能贖回的資產高於購買成本，即可從中獲利。

除了直接購買 YT 外，另一種作法為先於 Element 中存入資金，並將 PT 賣出，再將所得之現金重複存入 Element 內，反覆執行，以最大化手中 YT 數量。

Pendle

Pendle Finance 與 Element Finance 類似，也會將存入的資金拆分成本金代幣 (OT, Ownership Token) 和利息代幣 (YT, Yield Token)，主要的不同在於利息代幣運作機制。

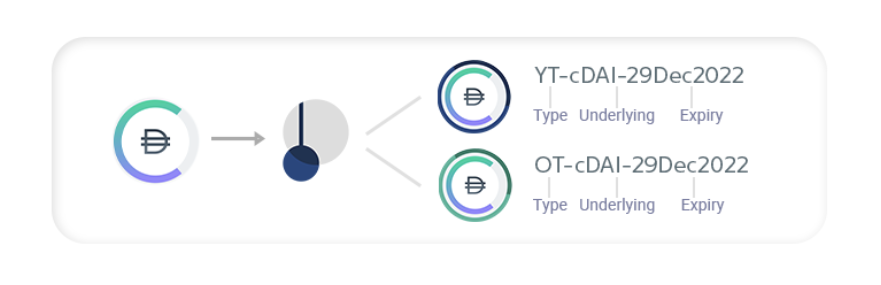
在 Element 中，本金產生的存款利息會累積於利息代幣內，累積的利息越多，結算後的贖回價就越高；而 Pendle 中本金產生的存款利息則會直接發放給利息代幣的持有人，持有利息代幣代表能擁有到期日前持續獲得利息收益的權利，而隨著到期日的接近，這個權利的時間價值會遞減，最終歸零。

• 固定利率存款
  若想在 Pendle 上實現固定利率存款，須先將資金存入協議中，鑄造出 OT 和 YT 後再將 YT 賣掉，提前套現未來利息，賺取固定之存款收益。
• 槓桿作多未來利率
  同樣的，對於看漲利率的投資人來說，也能透過購買 YT 來槓桿做多利率，只要 YT 的購買成本低於其產生出的利息即可從中獲利；或能透過存入資金，並將 OT 賣出，再把所得現金重新存入 Pendle 內，反覆執行前述步驟以最大化手中 YT 數量，加大做多利率之槓桿。
• 固定利率 AMM LP 交易手續費
  除了借貸協議與收益聚合器之外，Pendle 還支援以 Sushi LP token 作為底層資產，將未來因交易手續費而產生的收益代幣化，也同樣能以固定利率存款或槓桿做多未來利率。

Swivel

Swivel 前身為 DefiHedge，其原理一樣是將資金放入收益協議後，把資金拆分為本金 (zcTokens) 與利息(nTokens) 兩種代幣，透過在期初賣掉利息代幣，並保留本金代幣來獲得固定利率，而另一方利息代幣的持有者則得到浮動利率。存款利息與 Pendle 類似，會持續發放給利息代幣的持有者。

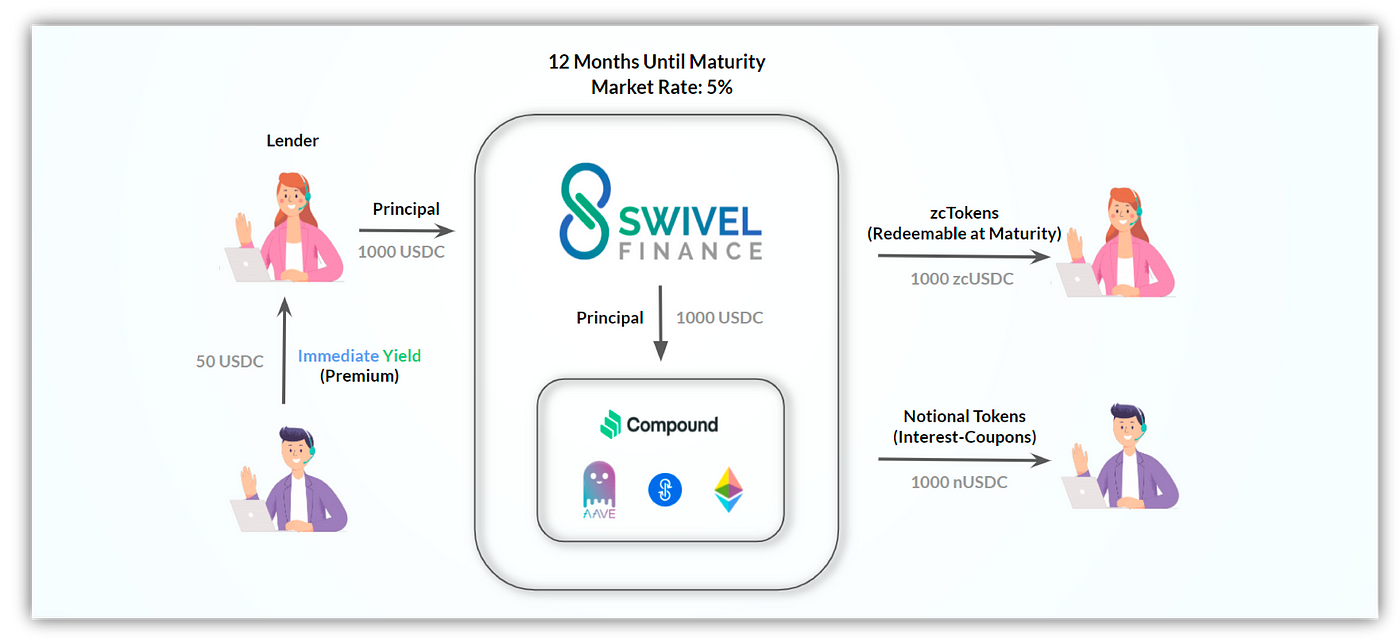
Swivel 與其他本息分離的協議最不一樣的特色在於，其他人都試著使用 AMM 來提供本金代幣與利息代幣的流動性，但他選擇了鏈下訂單簿來作為交易模型，其原因我們將在 AMM 章節深入討論。

Sense Protocol

Sense 延續一樣的模式，將資金拆分為本金代幣（Zeros）和 利息代幣（Claims），存款利息與 Pendle 類似，也會持續發放給利息代幣的持有者，但交易機制略有不同，我們將在 AMM Curve 章節進行更多比較。

---

結構型商品

分級基金（structured fund）又稱為結構化基金，他是通過對基金收益或是淨資產的分割與再分配，打造出不同等級風險收益不同的投資標的。常見情況是分為兩級，一級收取固定報酬，另一級則收取剩餘報酬。

假設我們稱「預期風險和收益均較低且優先享受收益分配的部分」為「A類份額」，另一類「預期風險和收益均較高但次後分配收益」的部分稱之為「B類份額」，B類份額本質是「借用」A類份額的資金來放大收益，而具備一定槓桿特性，也正是因為「借用」了資金，B類份額具支付A類份額約定利息的義務。

BarnBridge

BarnBridge 是利率結構型商品，由 Junior Pool 和 Senior Bond 組成。兩者的資金都會被投入到底層的協議（Compound, Aave）去產生利息，但收益分配的方式不同。

Junior Pool 的流動性提供者會拿到 ERC20 token，代表他的投資份額。Junior 沒有到期日，並且領取變動收益。而購買 Senior Bond 的人能自選投資時間（最長一年），倉位會以 ERC721 的形式持有，Senior 可以得到固定收益，但在到期日之前不能提早贖回，只能轉讓 NFT。

由於底層協議的利率是浮動的，有可能會忽然變很低。為了確保 Senior Bond 的持有者都能在到期時兌回承諾的本金和利息，Junior Pool 的部分流動性會被鎖定。因此，Junior 的贖回要經過特定的流程，有兩個選擇：

1. 立即贖回：預先扣除承諾要分給 Senior 的部分，剩下才能領回
2. 換成債券延後贖回：根據 Senior 的加權到期日 mint 出 NFT，到期日後才能贖回，不額外扣除費用

至於 Senior Bond 的利率則是透過以下公式決定：

其中 yield rate 是取 Compound/Aave 利率的三日平均值，再根據池內的流動性利用率打折，成為 Senior Yield。因為 Senior Yield 總是 <= 底層協議當下的利率，所以長期而言 Junior 可以賺取額外報酬，但是在利率忽然暴跌的時候可能出現少賺，甚至賠錢的情形。

Tranche

Tranche Finance 和 BarnBridge 類似，都是結構型產品，分成固定利率的 Tranche A 和浮動利率的 Tranche B（兩個都是 ERC20 token）。但不像 Barnbridge 會根據池中固定/浮動的比例決定利率，Tranche 完全沒有自動化的利率決定機制，取而代之的是由 DAO (token holder) 透過投票的方式「決定」要發給「固定」利率的人多少利息。所以本質上 Tranche A 並不是真的固定利率，隨時可能被投票改高或是改低利息。

可以看到 FIXED 和 VARIABLE 的利差很大，而且 governance 可以片面決定 FIXED 要改多少。

---

零息債券與本息代幣專用的 AMM

無論是零息債券、本金代幣或利息代幣，想要能在市場上被交易就會需要流動性。中心化交易所是以訂單撮合 (order matching) 的方式讓買賣雙方成交，流動性則是由買賣雙方掛單提供，此做法雖然可以讓價格發現的過程很有效率，但卻不適用於區塊鏈這種計算及儲存資源相對稀缺、效能較低的系統。因此在區塊鏈中，發展出了最適合 DeFi 世界的自動化做市商 (Automatic Market Maker, AMM)，AMM 的流動性會由買賣以外的第三方 — 流動性提供者 — 來提供，報價則由事前所規定好的數學關係式來決定。

不同的數學式會對應到不同的曲線，我們可以根據交易幣種的不同，設計出能給予合理報價的關係式。

以 Uniswap v2 為例，採用之恆定乘積做市商模型如下：

x × y = k

此曲線提供的邊際報價為 price = y/x，為池內兩個幣種之存貨比，當有交易發生而使存貨數量改變，價格就會隨之變化，此種模型適合價格波動較大的幣種。

另個極端的例子為 mStable，採用之恆定總和做市商模型如下：

x + y = k

此曲線提供之報價恆為 price = 1，無論池內兩幣種存貨如何改變，兌換比永遠為 1，適合貨幣價值完全相同之穩定幣互換。

然而，對於零息債券、本金代幣或利息代幣來說（本金代幣本質上是零息債券），他們有個共同的特性是「價值隨時間變化」，而以上兩種單純的 AMM 都沒有辦法很好反應這個特性。接下來我們將討論針對零息債券與利息代幣要如何設計好的 AMM 模型。

零息債券的定價和性質

零息債券的價格可由利率大小和到期時間來決定，他是以面額折價計算，也就是考量到未來現金流複利，折現到現在的價值為多少，公式如下：

債券價格 (PV) = 面額 (FV) ÷ (1 + r)^n

面額：債券的票面價值，到期後能拿到的金額
r：年利率
n：期數（年）

由以上定價公式可知，儘管市場利率不變，零息債券的價格仍會隨時間變化，越接近到期日，債券的價格就越接近面額大小，最終兩者之兌換率會收斂至 1。

從另個角度來看，若零息債券的價格維持不變，隨著到期日的接近，年利率 r 就會持續上升。

零息債券適合怎樣的 AMM 曲線

若以 Uniswap 的 x × y = k 作為 AMM 曲線，假若無人交易，池內狀態不變，零息債券的價格也會維持不變，則隨著到期日的接近 APY 就會不斷增加，而吸引人前來套利，使流動性提供者的承受損失；若使用 mStable 的x + y = k，則零息債券的價格永遠都為 1，無法在到期日之前折價交易，表現出時間價值。

由上可知，我們需要一條會隨時間演化而自動改變報價的曲線，讓零息債券的價格在一開始時對價格變化較敏感，能根據市場狀況改變，而越接近到期日兌換率會逐漸收斂至 1。

Yield Protocol 和 Notional 都是以購買或鑄造零息債券代幣來達到固定利率借貸的協議；Element, Pendle 與 Sense 則是將資產拆分成本金代幣和利息代幣，本金代幣本身也可以視為一種零息債券。以下簡介和分析前述五個協議使用之 AMM 曲線，最後討論不使用 AMM 而採用訂單簿的 Swivel。

YieldSpace

Yield Protocol 為了零息債券設計出了一條特製曲線 YieldSpace，該曲線之參數包含時間 t，t 越大代表距離到期日越遠，而隨著到期日的接近，t 會逐漸趨於零。

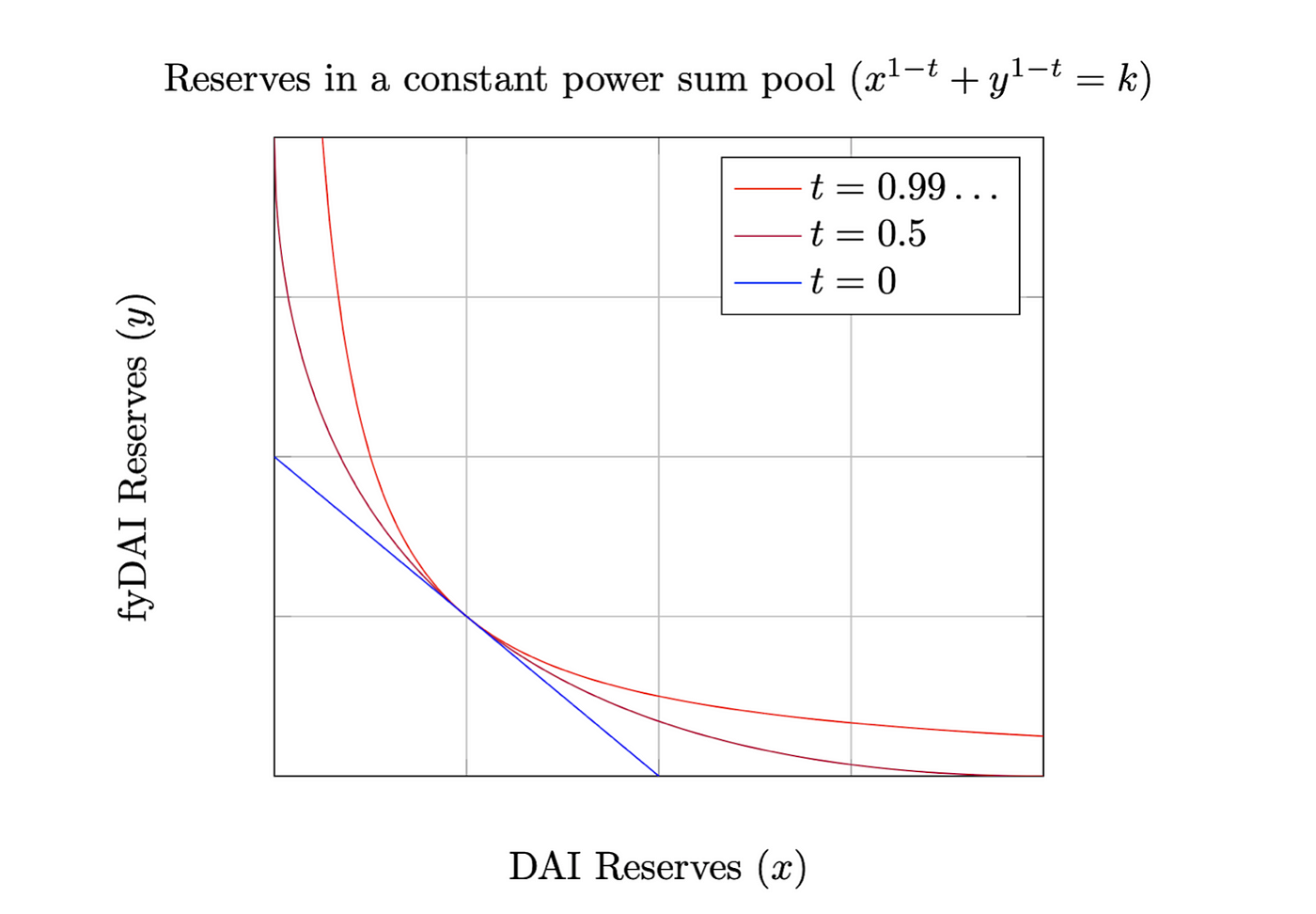
可由簡單的微積分證明此曲線於 t = 1 時會等價於 x × y = k而當 t = 0 時，曲線會演化成直線，變成 x + y = k。這讓使用者能於到期日之前，根據市場利率來交易債券，且當時間接近到期日，價格會自動接近 $1，最終可以 1:1 贖回債券面額資產，符合零息債券特性。

除此之外，YieldSpace 的曲線還有一個重要的性質為「利率恆定」。理論上，如果市場對於零息債券的供需沒有變化，零息債券的利率需要保持一致。供需沒有變化的意義對應到恆定乘積做市商模型 x × y = k ，意味著流動池內兩個幣種的存量不變，也因此其價格也保持不變。

然而，從零息債券的價格公式可得知，如果隨著時間變化，但要保持利率不變的話，得增加零息債券的價格，而 x × y = k 模型，無法自動反應零息債券的價格變化。而 YieldSpace 曲線具隨時間自動增加零息債券價格的特性，因此能帶來重要的「利率恆定」效果。

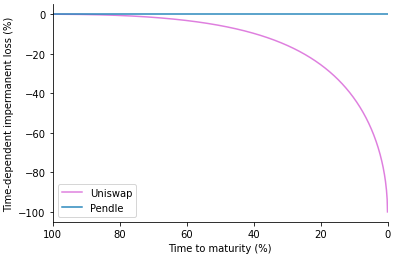
因此只要市場利率不變，都不會因時間造成的價格變化而產生套利空間，流動性提供者就不會有 time-dependent impermanent loss。

舉例來說，假設今有一檔一年期的零息債券，利率為 10%

初始價格為 $0.909 1 ÷ (1.1)^1 = 0.909
半年後價格為 $0.953 1 ÷ (1.1)^0.5 = 0.953
一年後價格為 $1 1 ÷ (1.1)^0 = 1

若都無人交易，代表池內兩幣種之存量（x,y）不變，並且市場利率維持 10%，六個月後，隨著 t 值變小，斜率相對改變，該零息債券的價格會上升至 $0.953；九個月後價格會再提升至 $0.976；最後到 $1。

動態手續費
現今主流的 AMM 都是以「交易量」之固定百分比做為手續費，如 Uniswap V2 手續費為 0.3%，而此機制不適用於零息債券的流動池，因為在到期日之前，0.3% 的手續費會對年化造成巨大的影響。

假設有一檔零息債券 APY 固定為 10%，則在不同時間以 0.3% 交易手續費交易，對年化利率之影響如下：

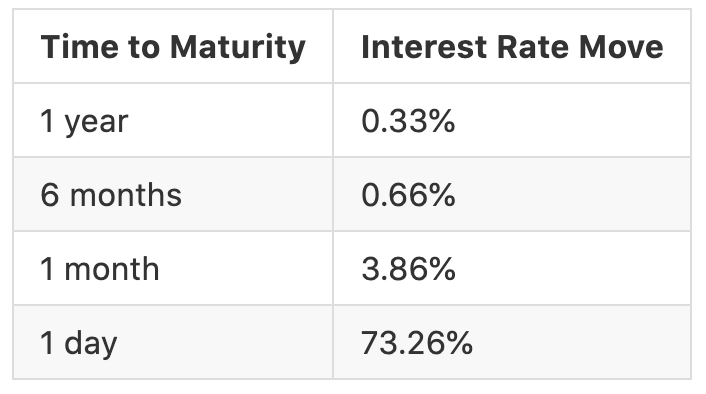
時間越接近到期日，手續費對年化利率的影響就越劇烈，該變化的大小會呈指數遞增。

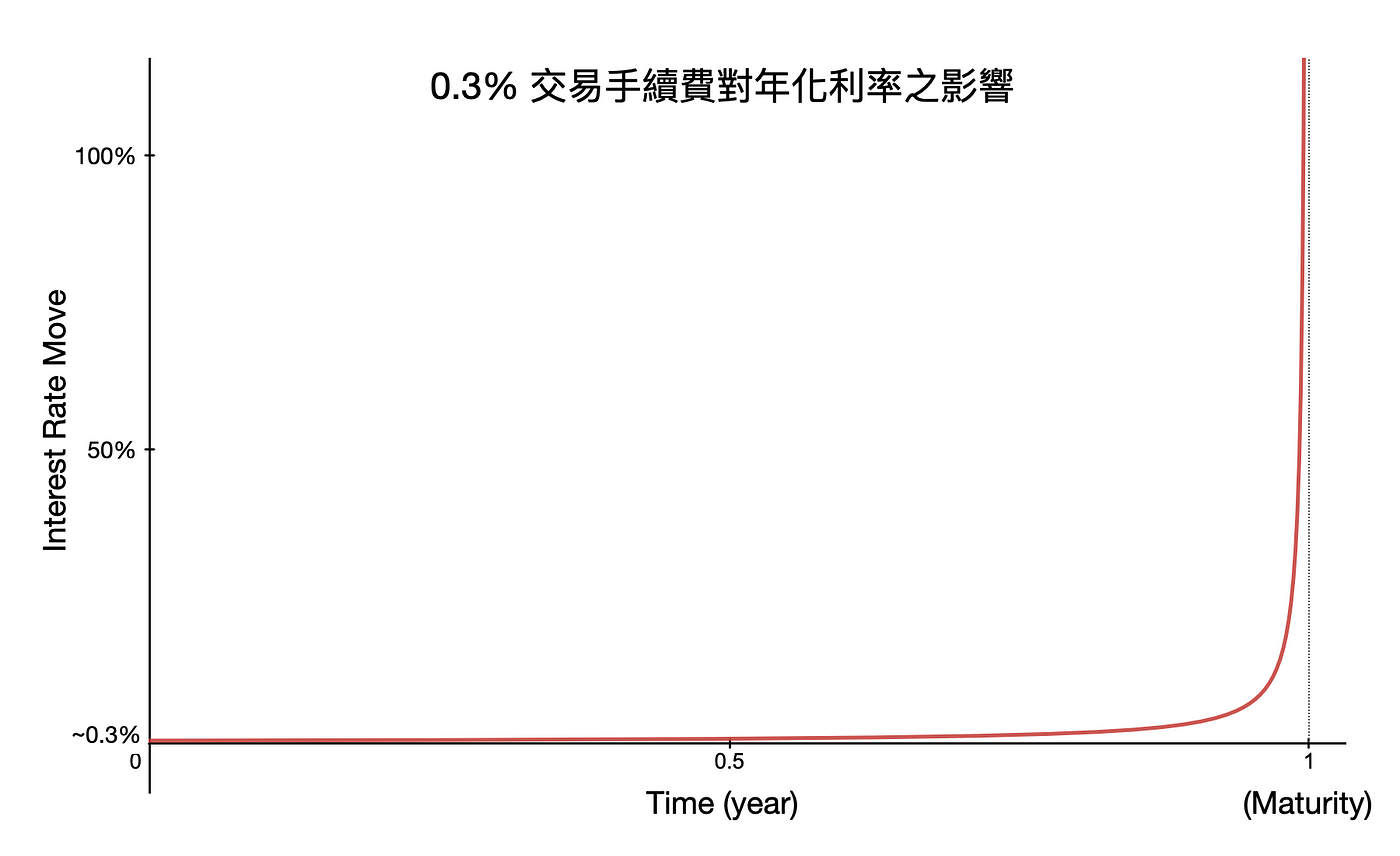
因此在 YieldSpace 中，手續費的計算改由「利息」中的固定百分比來收取，隨著到期日的接近，能產生的利息變少，交易手續費也會隨之降低。

虛擬流動性：增加資金效率
在正常的情況下，零息債券的價值永遠不該高於面額，也就是代幣的兌換率永遠不會超過 1，一旦超過即會創造出套利空間。

但在上述的 AMM 設計中，流動性的分佈會對稱於 x = y ，也就是兌換率為1 的兩側，但由於零息債券的價格不會超過 $1，代表流動池內有一半的資金永遠是閒置的，不會被交易到，因此 YieldSpace 引入了虛擬流動性，流動池內約一半的零息債券由虛擬存量 (virtual reserve) 提供，透過虛擬存量來讓此曲線能在不影響前述性質的情況下，大幅增大資金使用效率。

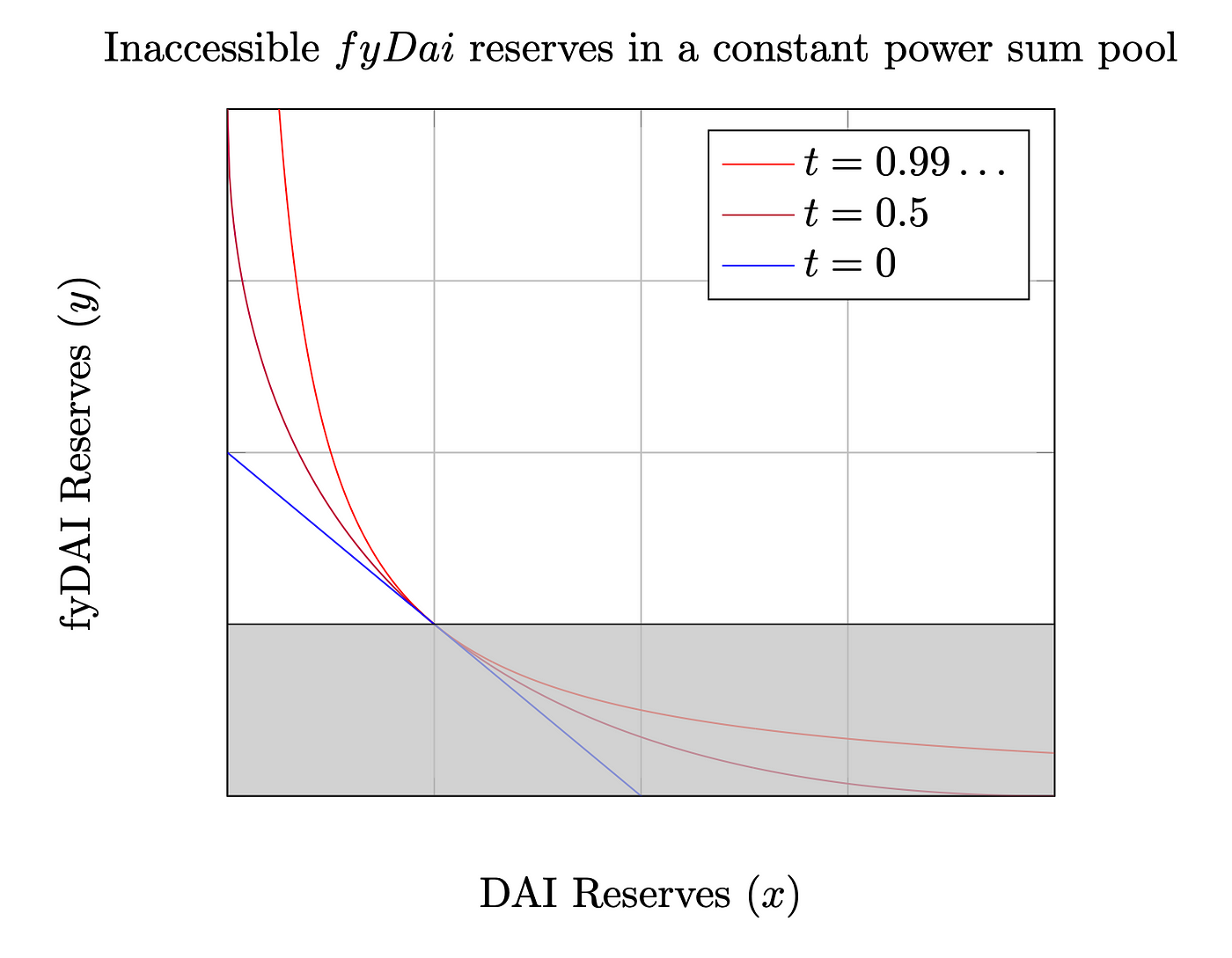
灰色區域為虛擬流動性，當 fyDAI 價格高於 1 DAI，系統不允許交易

Notional

由 YieldSpace 的討論中可了解到，作為一條適合零息債券流動池使用的 AMM 曲線需具備以下三個條件：

1. 儘管無人交易，系統能隨著到期日的接近自動調整價格，保持利率恆定。
2. 隨著到期日的接近，價格曲線需越來越平緩，使存量的變化對價格反應不敏感。
3. 手續費不能以固定百分比收取，需隨著到期日的接近降低

Notional 針對以上三個需求分別引入了以下三個參數：

Anchor
此參數控制價格曲線的中心，其兌換率 (fCash per Currency) 會隨著時間而減小，最終收斂至 1。

若不考慮交易造成的價格滑動，Anchor 的調整能使利率維持恆定，不讓時間的變化影響利率的大小。

Scalar
此參數代表價格對需求的敏感度，scalar 越小曲線越陡，價格變動越大。 隨著時間越接近到期日，曲線會越平滑，使流動性集中於 anchor 所錨定的價格中心。

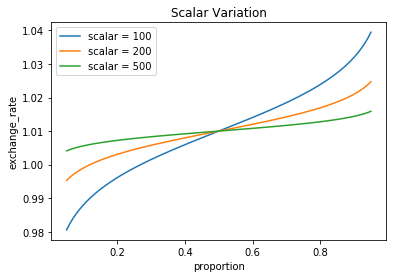
Trading Fee
手續費的大小會隨著時間線性遞減至零，以降低手續費對年化利息的影響

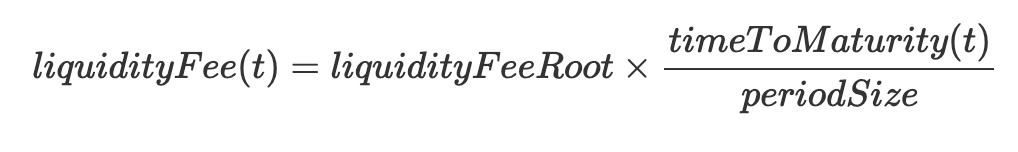
Notional AMM Curve

綜合以上三個參數可以得到 Notional AMM 的定價公式：

Element Finance

在 Element Finance 中，使用者存入的資金會被拆分成本金代幣和利息代幣，兩種代幣有不一樣的性質，因而會需要不同的流動池。

本金代幣池：
本金代幣為能在到期日後將本金贖回的憑證，相當於是零息債券，因此 Element 的本金代幣的流動池選擇使用 YieldSpace AMM 曲線。

利息代幣池：
利息代幣可在到期日時贖回期間內所累積的利息，但由於未來利息是不確定的，可能會因市場供需的變化而產生較大的價格變動，因此利息代幣的流動池選用 x × y = k 作為較容易做價格發現的曲線。

Pendle Finance

Pendle Finance 同樣為本金-利息拆分的模式，與 Element 的差異在於其利息代幣的運作模式，持有 Pendle 的 YT 代表領取存款利息的權利，持有越久可獲得越多收益，其價值會隨時間遞減至零。

本金代幣池：
Pendle 中的本金代幣性質也相當於是種零息債券，但卻沒採用 YieldSpace 或 Notional AMM 這類適合零息債券使用之 AMM，而是選了 SushiSwap 作為流動池。

SushiSwap 使用恆定乘積做市商作為模型，該曲線不會隨著時間而變動，代表流動性提供者會隨著時間變化必然會產生暫時性損失。而採用 SushiSwap 作為流動池也就意味著 Pendle 放棄「以 OT 作為零息債券來使用」之性質，讓固定利率存款的過程變更複雜，使用者體驗變差，可謂相當可惜。

利息代幣池：
Pendle 中 YT 在到期時價值必然歸零，若以 x × y = k 做為 AMM 曲線，則隨著時間的流逝，利息代幣的時間價值遞減，會吸引套利者前來套利，而造成流動性提供者的損失，最終使整個流動池的價值歸零。

為解決上述問題，Pendle 參考了 Balancer 的曲線，並多引入了時間相關之參數，使兩個幣種的權重會隨時間而改變。

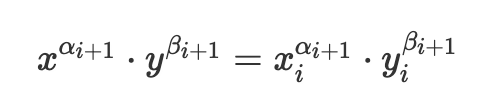
αi+1： x 於時間 t = i + 1 之權重βi+1： y 於時間 t = i + 1 之權重xi 和 yi 為時間 t = i 時流動池內之存量

α 和 β 皆為時間的函數，會隨時間變化。

在初始 t=0 時 α 和 β 皆為 0.5，隨著時間接近到期日，α 會逐漸變小，最終為 0；β 則會逐漸變大，最終為 1。

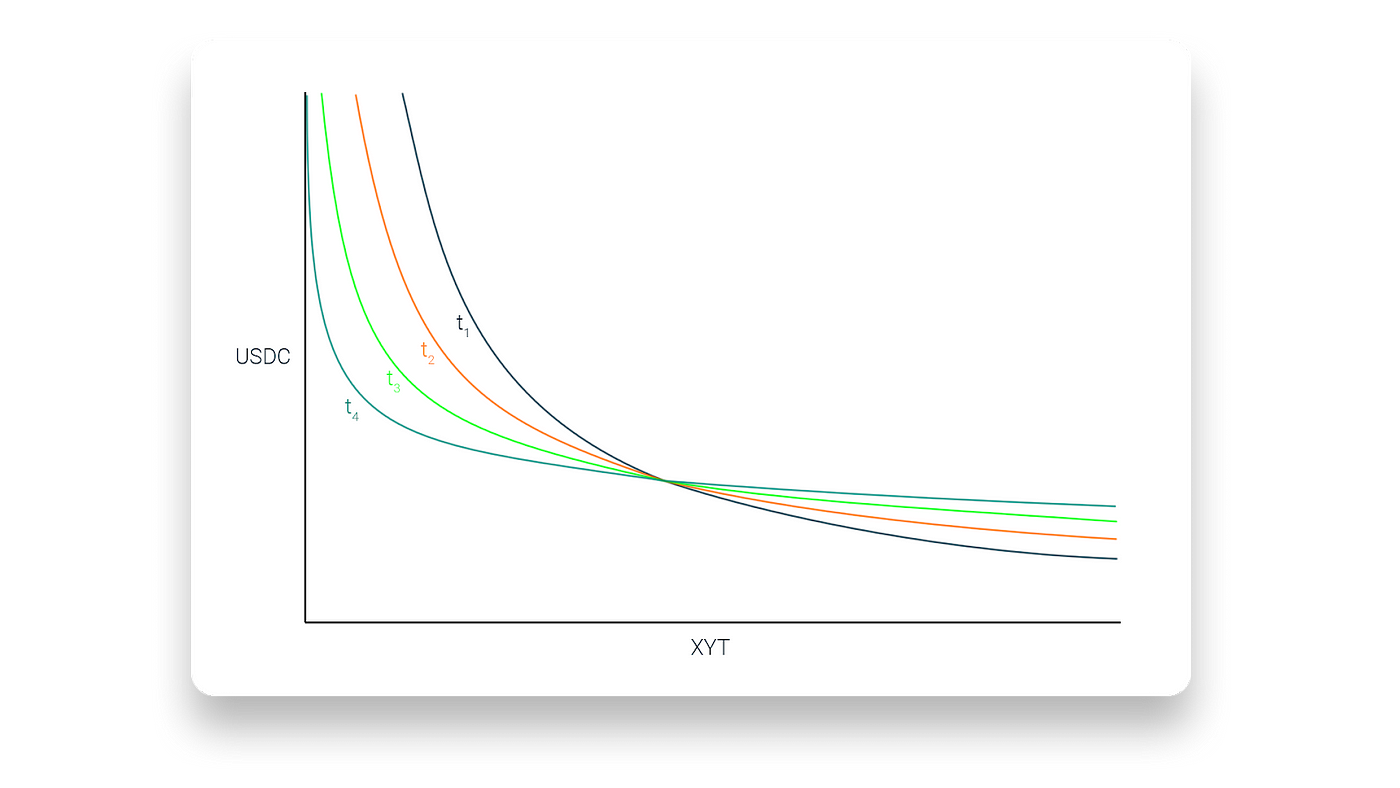
以利息代幣 YT/USDC 池為例，在開始時兩個幣種之權重比為 50/50，此時 YT 的價格為 $1，隨著到期日的接近，YT 的權重會逐漸下降，當權重比下降至 20/80 時，若這段時間無人來交易，則 YT 的價會變為 $1 ⨉ (20/80) = $0.25，而最終比例會變為 0/100，此時的 YT 價格即為 $0。

由以上說明可知，此 AMM 曲線能動態的調整報價，符合代幣價值隨時間遞減之性質，以避免流動性提供者承受 time-depedent impermanent loss。

Sense Protocol

Sense 作為另個本金-利息分離型的固定利率協議，其本金代幣 (zcToken) 之性質也相當於是零息債券，而其流動池採用 Sense Space AMM，為前述之 YieldSpace AMM 的改良版。

Sense Space

本金代幣池：
Sense Space 使用了 YieldSpace 之恆等式，但將其中的標的資產 (underlying asset) 更換成利率收益資產（yield-bearing asset），讓流動池內的每種資產都能隨時間產生價值，最大化資金效率。

但由於 YieldSpace 的 AMM 曲線會將流動性集中至 1:1 附近，以 zcDAI/DAI 池為例，若只將 DAI 改成 cDAI 作為零息債券的配對資產，則 AMM 無法如期運作。為了解決此問題，Sense Space 多引入了 scaling factor，此參數為 Compound 中 cDAI 對 DAI 的兌換比。如此一來，無論是交易或增加、移除流動性，只要先透過該參數將 cDAI 的價值對應回 DAI 的數量後，就能以 YieldSpace 的公式計算兌換率。

實作方面，合約會於初始化時記錄下 cDAI 與 DAI 的兌換率，並於每次交易時更新此參數，如此還能確保 cDAI 利息的累積不會影響零息債券 (zcDAI) 的美元兌換價值。

利息代幣交易：
Sense 的利息代幣設計採用 Pendle 的模式 (Collect YT)，但只提供 PT/Target 交易對（Target 在 Sence 中意指利率收益資產）而沒提供 YT 流動池。

如果要交易 YT 則需要利用 Target = PT + YT 的關係來兌換。舉例來說，在 Sence 上，如果想要購買 Compound Dai 的利息代幣（YT）：

1. 存入 cDai 得到本金代幣 zcDai + 利息代幣 ccDAI
2. 將 zcDai 交易換成 cDai
3. 此時手上會剩下 zcDai 跟剩餘的 cDai，可以重複步驟 1~2 ，盡量把 cDai 都換成 zcDai

反過來，若你要賣掉利息代幣：

1. 跟 Pool 閃電貸出 cDai
2. 把 cDai 換成本金代幣 zcDai
3. 把手上的利息代幣 ccDAI 與借來的 本金代幣 zcDai 合成贖回 cDai
4. 把閃電貸借出的 cDai 還回去
5. 手上會剩下一部分 cDai

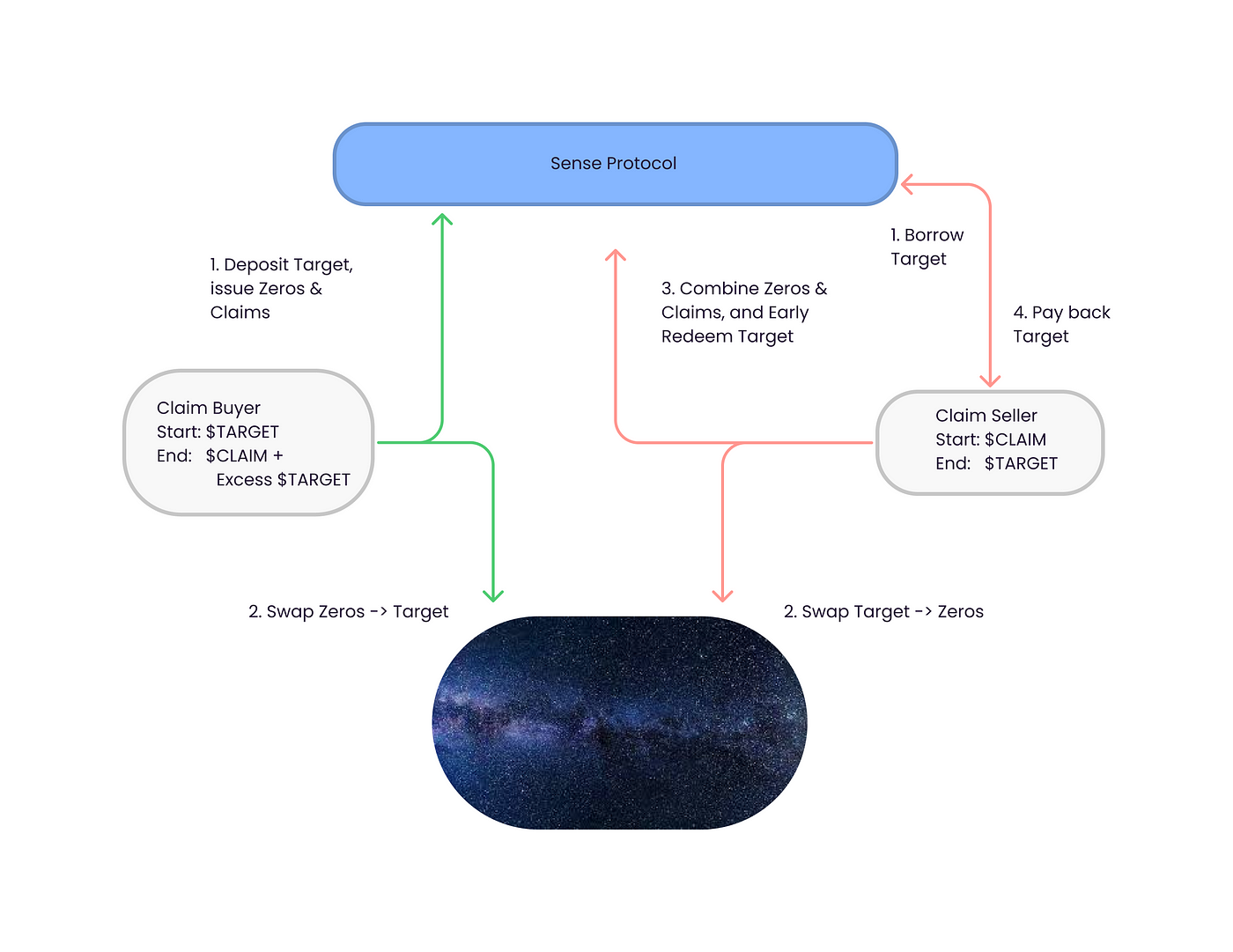
要成為流動性提供者，也是用類似的方式入池，可以看見以上的方法好處是，我們只需要有一個 本金代幣 — 利率收益資產 AMM 池，不需要設計利息代幣的交易模型，因此原本兩池的流動性能聚合在同一池，進而提高 LP 從交易量而賺得的收益，但很明顯的代價是交易的運算過程變複雜了，不僅難以將手上的利率收益資產毫無剩餘地購買利息代幣，同時也要付出更多 gas 。

另闢蹊徑的 Swivel

最後，身為唯一一個不使用 AMM 定價的協議 ，Swivel 選擇以鏈下訂單簿的機制來解決本金與利息代幣在 AMM 上定價困難。

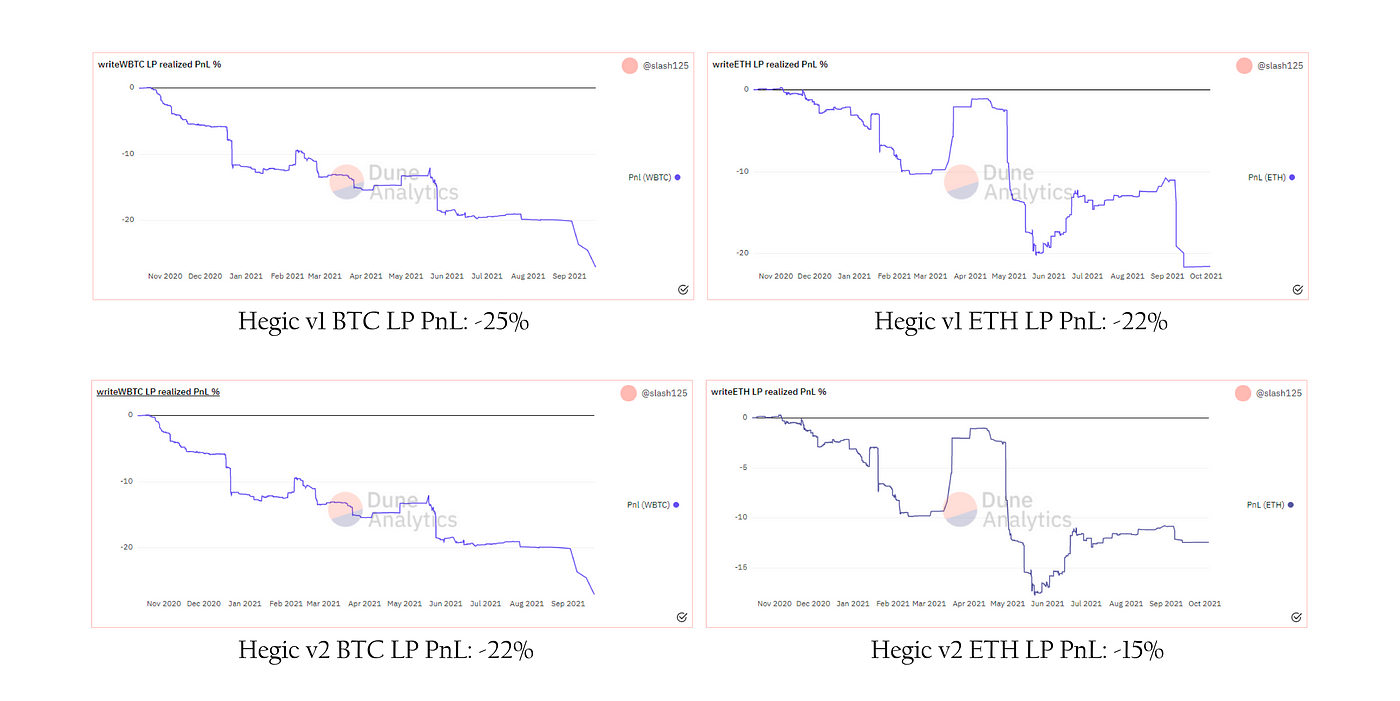
Swivel 認為利息代幣等作為利率的衍生品，其價值會隨著利率和利率波動的變化，但 AMM 中的利息代幣價格難以立刻反應變化。相同的現象也存在於現貨市場與其衍生品之間，在選擇權市場中，選擇權價格不斷對現貨價格和現貨波動做出反應，若要用 AMM 實現 DeFi 選擇權市場，其 AMM 模型也必須以某種方式適應這些因素改變。選擇權 AMM 雖然發展迅速，但仍難以考慮即時波動性，這導致流動性提供者 (LP) 的回報極低，在 Swivel 對 DeFi 選擇權協議 Hegic 的流動性提供者分析中，能發現他們承受了巨大的損失。

因此 Swivel 認為訂單簿比起 AMM 適合做衍生品的 DeFi 交易模型，不僅能讓 Market Maker 避免定價失真所帶來的損失，同時為使用戶提供最優惠的價格和最低的交易成本。除此之外，還可以提供本金代幣-利息代幣的訂單簿交易對，讓使用者能直接交換兩者，不需要像 Element 一樣得在兩個 AMM 上做交易 (YT-Underlying & PT-Underlying)，增加了交易的效率。

---

資金效率問題和市場效率問題

各個協議實作固定利率的方式略有不同，也因此在「資金效率」和「市場效率」上各有優點和缺點。

固定利率借貸 v.s. 收益重分配

Yield/Notional 的零息債券和 Element/Pendle 的本金代幣的性質非常接近，機制卻大不相同。

Element 最大的缺點是價格發現的效率非常糟糕，它需要為本金代幣和利息代幣分別建立流動池，需要更多資金提供流動性。另外，想得到本金代幣有兩種路徑，一個是用現金鑄造出 PT + YT 再賣掉 YT，另一個是直接現金買 PT。理論上，在足夠有效率的市場，兩種路徑的產出應該要是完全一樣的，但區塊鏈的限制加上 AMM 的特性卻會讓兩者很容易有差額，顯得很沒效率。

相較於 Element 有兩種路徑交易本金代幣，因此有利差套利問題， Yield 直接了當，只有零息債券交易池，由借貸雙方對折現（利息）供需共識來決定價格。但可惜有一好就沒兩好，Yield、Notional 等固定利率借款方法本質上是一個獨立的「初級」借貸市場，不像 Element、Pendle 等本息分離協議，是架構在現有借貸協議上的利率「次級」市場。固定利率借貸類型協議中，利率的市場均衡是仰賴自身流動池的供需比例來決定，而非已經有大量流動性的底層利率協議。同時作為一個新興的借貸市場，得自己重新聚籠資金來創造流動性，相對來說供給/需求彈性會明顯較差，若出現供需嚴重失衡的現象，例如大量存款進入 Yield 購買零息債券，讓 Yield 的利率相對於外部利率市場 Compound/Aave 大幅降低時，會需要更久的時間才能達到新平衡。

提升市場效率

值得一提的是 Notional 和 Swivel 對提升效率的嘗試。

Notional 的流動性提供者不需要「分配」資金到不同到期日的池子，並於到期後手動將資金贖回，而是集中所有資金進到一個大池，再由治理的方式根據市場需求統一調度流動性。如此可讓閒置資金發揮更大的功效，提升市場效率也增加流動性提供者的收益。

Swivel 則是直接捨棄 AMM 改用 orderbook，論述大致上也算合理，利率市場和選擇權市場類似，複雜到不適合用 AMM 的形式處理。但這裡有個關鍵點是利率市場的 PnL 不高，所以對交易成本格外敏感，如果 Swivel 因為鏈下訂單簿的限制造成取消/更新 order 的成本很高，恐怕會抵銷它高資本效率的優勢。

提升資金效率

另一方面，做零息債券的 LP 可能存在著某種本質上的矛盾，因為會想持有這類資產的人理論上就是想賺利息，但流動池中必須有一些現金是沒在生利息的。甚至 YieldSpace 為了效率砍掉了一半用不到的流動性，正好就是零息債券的那部分，讓池子的平均利率又更低了。所以對 LP 而言，除非交易手續費超過零息債券的利率，否則沒有理由把錢分配在 AMM 而不是買債券。

因此 Sense 提出用利率收益資產來與零息債券配對做 LP，讓流動池的現金以生息資產的形式存放，但其代價為是使用者進出時，需要多做一層轉換增加 gas 的開銷。

結構型商品 BarnBridge 的固定利率 NFT 發行並不仰賴 AMM，而是直接在系統內部完成價格發現，最大的好處就是生態中的所有角色的所有資金都處在生利息的狀態，沒有一絲一毫閒置資金，不過這也不是全無代價的。

從市場構成的角度來看，「固定利率借貸」和「本金-利息分離」是利率的 long-short market，結構型利率協議則是利率的 hedge-speculate market。前者才是比較自然的供需關係，後者的 speculate part 並不是正常的需求，他是為了滿足一方想 hedge 而讓另一方 take risk 而生。做為對沖風險服務的提供者，對沖風險方的交易對手會希望收到超額報酬，所以長期而言 BarnBridge sBOND 的利率很可能會低於 Yield/Element 的零息債券的利率。

下一步：利率衍生品

在前面的分析中我們反覆強調效率的重要性，是因為利率市場對交易成本非常敏感。對於一年可以 +100% 的比特幣來說，0.6% 的交易摩擦似乎不算什麼，但對於 4% APR 的零息債券而言，那是高達獲利的 15% 成本！

但話說回來，我們希望從浮動利率過渡到固定利率的真正目的是為了對利率波動避險（或投機）。進一步來說，我們關心的是借/存錢一段時間的實際利率是否和當初預期的相同。真正需要被交易的既不是本金、也不是利息，而是「利差」。

上面介紹到的幾個協議產生固定利率的方式略有不同，但都可以視為是利率的現貨市場，直觀，但效率低下。在利率衍生品市場，我們只需要一點點保證金就可以交易同樣名義金額資產的利率。少了本金，對交易摩擦的容忍就變高了，也不需要鎖倉大量資本在 AMM 來提供流動性，效率高非常多。

下一章，我們將詳細分析利率衍生品的優點，並介紹 Hakka Finance 推出的 iGain — Interest Rate Synth，一款基於利率交換的金融衍生工具。

參考資料：

• Aave GitBook: Interest Rate Model
• Yield Protocol Docs
• YieldSpace AMM Whitepaper
• Notional Docs
• Hifi Docs
• Element Finance Docs
• Element Finance Whitepaper
• Pendle Finance Litepaper
• Pendle AMM Design Paper
• Swivel Docs
• Swivel Blog
• Sense Medium: Introducing Sense Space
• Sense Medium: Designing Yield Tokens
• Sense Docs: User Journeys
• BarnBridge Docs
• Tranche Docs
• Aavescan

---

Hakka.Finance | Discord | Wiki | Medium | Twitter | Telegram | Job